这篇博客用于提醒自己在写算法题时，很容易忽视的易错点，有时明明是很小的问题，却花了好长时间才发现。

2024/12/10 要考试了，此博客除了易错点整理外，还整理了各种算法思想来应对考试！例题是选取pta上面我提交了好几次才ac的题目。┭┮﹏┭┮

一、易错点

1.qsort的cmp函数

如下图代码，a.d 和b.d都是double类型,如果return语句是a.d-b.d，那么当a.d和b.d的整数位的值相同时，它们并不会排序，导致排序有问题。

1
2
3
4
5
6
7
8
9
int cmp(const void * x, const void * y){
    struct map a = *(struct map*)x;
    struct map b = *(struct map*)y;
    if(a.d > b.d){
        return 1;
    }else{
        return -1;
    }
}

2.memset函数

void *memset(void *str, int c, size_t n)

str是数组名，c是数值，n是sizeof(数组名)

例如：memset(arr, 0, sizeof(arr));

memset对于char数组，可以任意c赋值，而int数组只能用于赋值0。因为它是按字节赋值的。

参考链接memset()函数的用法详解-CSDN博客

3.strcmp函数

4.c++的队列对象

5.qsort函数

qsort函数包含四个参数，分别是：

1.数组名

2.元素个数（从前往后计算）

3.数组元素所占字节（int，double，char等所占字节）

4.排序原则（递增，递减，奇偶交叉等）

使用例子：

int arr[100];

qsort(arr, n, sizeof(int), cmp);

参考链接C语言排序神器——qsort函数（看这一篇，足矣）-CSDN博客

二、算法整理

1.背包问题

1）普通的0-1背包问题

直接根据动态规划来做

但是，注意，有时会有坑，比如如下代码，问题出在第18行，j应该是>=0,而不是>0,原因是vol[i]可能为0.

因为题目的输入要求为

第一行包含整数 T ，即个案数。后面是 T 个案例，每个案例有三行，第一行包含两个整数 N ， V ， （N <= 1000 ， V <= 1000 ） 代表骨头的数量和他的袋子的体积。第二行包含 N 个整数，表示每个骨骼的值。第三行包含 N 个整数，表示每个骨骼的体积。

这里V没有说大于0，所以0也是可能的。真的吐了，检查了半天，也太恶心了，正常来说肯定大于0啊。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int main(){
    int t, n, v;
    int val[1111] = {0}, vol[1111] = {0};
    int dp[1111] = {0};
    scanf("%d", &t);
    while(t-- > 0){
        memset(val, 0, sizeof(val));
        memset(vol, 0, sizeof(vol));
        memset(dp, 0, sizeof(dp));
        scanf("%d %d", &n, &v);
        for(int i = 1; i <= n; i++){
            scanf("%d", &val[i]);
        }
        for(int i = 1; i <= n; i++){
            scanf("%d", &vol[i]);
        }
        for(int i = 1; i <= n; i++){
            for(int j = v; j > 0; j--){
                if(j >= vol[i])
                    dp[j] = max(dp[j], dp[j-vol[i]] + val[i]);
            }
        }
        printf("%d\n", dp[v]);
    }
}

2）普通的完全背包问题

即可以取任意个相同的物品，应该对于每一个物品，都把它遍历至容量结束为止，可以参考如下代码。

题目链接湫湫系列故事——减肥记I(HDU-4808)-CSDN博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main(){
    int n, m;
    int a[111], b[111];
    while(scanf("%d", &n) != EOF){
        for(int i = 1; i <= n; i++){
            scanf("%d %d", &a[i], &b[i]);
        }
        int dp[111111] = {0};
        scanf("%d", &m);
        for(int i = 1; i <= n; i++){
            for(int j = b[i]; j <= m; j ++){
                    dp[j] = max(dp[j], dp[j-b[i]] + a[i]);
            }
        }
        printf("%d\n", dp[m]);
        }
}

3）对于判断是否装满背包的完全背包情况下

得最大/最小的价值情况，要额外进行判段，给每一个物品从头遍历至容量最大值时，先判断该容量是否可以装满，可以则进行赋值，不行则不管它。

题目链接Piggy-Bank HDU - 1114 （完全背包模板题）_在acm能够做任何事情之前,必须编制预算并获得必要的财政支持。这一行动的主要收入-CSDN博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int main(){
    int p[600], w[600];
    int dp[11000];
	scanf("%d", &t);
    while(t -- > 0){

        scanf("%d %d", &e, &f);
        f = f - e;
        scanf("%d", &n);
        for(int i = 0; i <= f; i++){
            dp[i] = INF;
        }
        for(int i = 1; i <= n; i++){
            scanf("%d %d", &p[i], &w[i]);
        }
        dp[0] = 0;
        for(int i = 1; i <= n; i++){
            for(int j = w[i]; j <= f; j++){
                if(dp[j - w[i]] != INF){
                    dp[j] = min(dp[j], dp[j-w[i]] + p[i]);
                }
            }
        }
        if(dp[f] != INF){
            printf("The minimum amount of money in the piggy-bank is %d.\n", dp[f]);
        }
        else{
            printf("This is impossible.\n");
        }
	}
}

4）对于普通背包问题，不要进行额外判断了，会出错

和第二点的题目一样，但使用了额外判断时不能通过。

未通过代码如下，原因是，从后找能完全符合容量的幸福度不一定是最大的，这是因为占满容量的限制。导致越大的容量价值不一定最高。

例如 价值 容量

​ 111 100

​ 1 123

这个情况下，123容量装满只有1元，而100容量装满有111元。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<stdio.h>
#include<stdlib.h>

int max(int x, int y){
    if(x > y)
        return x;
    return y;
}
int main(){
    int n, m;
    int a[111], b[111];
    while(scanf("%d", &n) != EOF){
        for(int i = 1; i <= n; i++){
            scanf("%d %d", &a[i], &b[i]);
        }
        int dp[111111];
        for(int i = 0; i < 111111; i++){
            dp[i] = -1;
        }
        dp[0] = 0;
        scanf("%d", &m);
        for(int i = 1; i <= n; i++){
            for(int j = b[i]; j <= m; j ++){
                if(dp[j - b[i]] != -1)
                    dp[j] = max(dp[j], dp[j-b[i]] + a[i]);
            }
        }
        if(dp[m] != -1)
            printf("%d\n", dp[m]);
        else{
            for(int i = m - 1; i >= 0; i--){
                if(dp[i] != -1){
                    printf("%d", dp[i]);
                    break;}
            }
        }
    }
}

2.放挡板法

核心思想，数量最多的种类的数量值 - 1<=总数-数量最多的种类的数量值时，才可以将同种类的物品都隔开。

例题，吃糖果

HOHO，终于从Speakless手上赢走了所有的糖果，是Gardon吃糖果时有个特殊的癖好，就是不喜欢将一样的糖果放在一起吃，喜欢先吃一种，下一次吃另一种，这样； 可是Gardon不知道是否存在一种吃糖果的顺序使得他能把所有糖果都吃完？ 请你写个程序帮忙计算一下。

输入格式:

第一行有一个整数T，接下来T组数据，每组数据占2行，第一行是一个整数N（0<N<=1000000)，第二行是N个数，表示N种糖果的数目Mi(0<Mi<=1000000)。

输出格式:

对于每组数据，输出一行，包含一个”Yes”或者”No”。

输入样例:

1
2
3
4
5
2
3
4 1 1
5
5 4 3 2 1

输出样例:

1
2
No
Yes

答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<stdio.h>
int main(void)
{
	int t;
	scanf("%d", &t);
	while (t--)
	{
		int n, num;
		//long long保险，毕竟有可能要加很多数，有很大几率超出int
		long long sum = 0;
		//最大值假定-1完美没问题，因为题目输入都是自然数
		int max = -1;
		scanf("%d", &n);
		while (n--)
		{
			scanf("%d", &num);
			if (max < num)
				max = num;
			sum += num;
		}
		//个人感觉这个写法容易理解
		if (sum - max <= max - 2)
		//sum - max < max - 1
		//sum - max + 1 < max
		//都是等价的
			printf("No\n");
		else
			printf("Yes\n");
	}
	return 0;
}

3.贪心

核心思想：每次都先取最优解

例题，田忌赛马

输入格式:

输入最多包含 50 个测试用例。每个情况都以第一行的正整数 n （n <= 1000） 开始，这是每边的马匹数量。第二行接下来的 n 个整数是 Tian 的马的速度。然后第三行的下一个 n 个整数是国王的马的速度。input 以一行结尾，该行在最后一个测试用例后有一个 0。

输出格式:

对于每个 Importing case，输出一行包含单个数字的行，这是 Tian Ji 将获得的最大金额，以银元为单位。

输入样例:

1
2
3
4
5
6
7
8
9
10
3
92 83 71
95 87 74
2
20 20
20 20
2
20 19
22 18
0

输出样例:

1
2
3
200
0
0

思路

用田忌最快的马与王最快的马相比较

如果田忌的快马比王的快马要快

果断把先用田忌的快马先赢一把(这样赢是代价最小的)

如果田忌的快马比王的快马要慢

果断把最慢的马与王最快的马比赛(因为反正都要输，这样我输的价值更大，因为我把最快的马比下去了，可以增加后面其他马赢的机会)

如果田忌的快马与王的快马速度一样——重点！！！

拿田忌最慢的马和王最慢的马比较

慢马能赢就让慢马赢，直到慢马比王的慢马速度一样或者更慢时，让慢马和王的快马比，

之所以慢马速度相同时依旧要让慢马输给快马的原因是如下情况

王 90 80 70

田忌 90 80 70

这时候，如果慢马比掉快马，田忌后面两只都能赢，最后得分200，但如果慢马依旧和慢马比，得分最后是0。

此外，还需要判断，是否慢吗和快马的速度一样，因为有可能是如下形式

王 90 90 90

田忌 90 90 90

这种情况，不需要减得分。

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<stdio.h>
#include<stdlib.h>
int cmp(const void *a, const void *b){
    int n1 = *(int*)a;
    int n2 = *(int*)b;
    return n2 - n1;
}
int main(){
    while(1){
        int num;
        scanf("%d", &num);
        if(num == 0)
            break;
        int tianji[num];
        int king[num];
        for(int i = 0; i< num; i++){
            scanf("%d", &tianji[i]);
        }
        for(int i = 0; i < num; i++){
            scanf("%d", &king[i]);
        }
        qsort(tianji, num, sizeof(int), cmp);
        qsort(king, num, sizeof(int), cmp);
        int end = num - 1;
        int top = 0;
        int score = 0;
        for(int i = 0; i < num; i++){
            if(king[i] > tianji[top]){
                score -= 200;
                end -= 1;
            }else if(king[i] < tianji[top]){
                score += 200;
                top += 1;
            }else{
                //慢马能赢就让它赢
                if(tianji[end] > king[num-1]){
                    score+= 200;
                    end -= 1;
                    num-= 1;
                    i -= 1;
                }else if(tianji[end] == king[i]){
                    end -= 1; //慢吗和王的快马的速度一样时不需要减得分
                }else{
                    score -= 200; //慢马和王的慢马速度一样或者更慢，且慢马比对面快马慢时，需要减得分
                    end -= 1;
                }
            }
        }
        printf("%d\n", score);
    }
}

4.递归

核心思想：确立后续

例题一、母牛的故事

有一头母牛，它每年年初生一头小母牛。 每头小母牛从第四个年头开始，每年年初也生一头小母牛。 请编程实现在第n年的时候，共有多少头母牛？

输入格式:

输入数据由多个测试实例组成，每个测试实例占一行，包括一个整数n(0<n<55)，n的含义如题目中描述。
n=0表示输入数据的结束，不做处理。

输出格式:

对于每个测试实例，输出在第n年的时候母牛的数量。
每个输出占一行。

输入样例:

1
2
3
4
2
4
5
0

输出样例:

1
2
3
2
4
6

答案

解法：n年母牛的数量等于n-1年母牛的数量加上n-3年母牛的数量，因为n-3年的所有母牛到n年都已经成年了，所以第n年出生的母牛等于n-3年的母牛数量。而第n年的母牛数量等于去年母牛数量加新生母牛数量。故可得递推式m[n] = m[n-1] + m[n-3]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<stdio.h>
#include<stdlib.h>
int main(){
    long long m[55];
    m[1] = 1;
    m[2] = 2;
    m[3] = 3;
    m[4] = 4;
    for(int i = 5; i < 55; i++){
        m[i] = m[i - 1] + m[i - 3];
    }
    while(1){
        int n;
        scanf("%d", &n);
        if(n == 0){
            break;
        }
        printf("%lld\n", m[n]);
    }
}

例题二、儿童队列

PHT School 有很多学生。有一天，名叫 PigHeader 的校长希望所有学生站成一排。他规定女孩不能单身。换句话说，要么队列中没有女孩，要么不止一个女孩并排站着。情况 n=4（n 是孩子的数量）类似于
FFFF、FFFM、MFFF、FFMM、MFFM、MMFF、MMMM
这里 F 代表女孩，M 代表男孩。满足校长需求的队列总数为 7。你能做一个程序来找到有 n 个孩子的队列总数吗？

输入格式:

此问题有多种情况，并由 EOF 结束。在每种情况下，只有一个整数 n 表示子项的数量 （1<=n<=1000）

输出格式:

对于每个测试用例，只有一个整数表示满足 Headmaster 需求的队列数量。

输入样例:

1
2
3
1
2
3

输出样例:

1
2
3
1
2
4

答案

解法：

设f[n]合法

前提，队尾是M,那么前面一定要合法，因为非法无法变成合法。若队伍最后两位是MF,那么只有去掉最后两位后是合法，且该队伍继续进入的下一位是F的情况非法才能变为合法。

当f[n]的队尾是M时，前n-1个数肯定合法，所以f[n] 的数量等于 f[n-1] 的数量

当f[n]的队尾是F时，要求f[n]合法，所以f[n-1]的队尾是F.

此时，f[n-2]既可以合法又可以非法

f[n-2]合法时，f[n]的数量等于f[n-2].

而f[n-2]非法时，f[n-2]的队尾两个元素为MF。所以f[n-4]是合法的，f[n]数量等于f[n-4]

综上三种情况整合起来，得递推式f[n] = f[n-1] + f[n-2] + f[n-4]。

此外，本题还要求高精度，超过了long long，所以用了二维数组来存值每个十进制位的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<stdio.h>
#include<stdlib.h>
int main(){
    long long f[1001][101] ={0};
    f[0][1] = 1;
    f[1][1] = 1;
    f[2][1] = 2;
    f[3][1] = 4;
    f[4][1] = 7;
    for(int i = 5; i < 1001; i++){
        int add =0;
        for(int j = 1; j <= 100; j++){
            f[i][j] = add + f[i - 1][j] + f[i - 2][j] + f[i - 4][j];
            add = f[i][j] / 10000;
            f[i][j] = f[i][j] % 10000;
            if(add == 0 && f[i][j] == 0){
                break;
            }
        }
    }
    int k;
    while(scanf("%d", &k) != EOF){
        int end = 0;
        for(int i = 100; i  > 0; i--){
            if(f[k][i] != 0){
                end = i;
                break;
            }
        }
        printf("%d", f[k][end--]);
        for(int j = end; j > 0; j--){
            printf("%04d", f[k][j]);
        }
        printf("\n");
    }
}

5.动态规划

例题一、免费馅饼

都说天上不会掉馅饼，但有一天gameboy正走在回家的小径上，忽然天上掉下大把大把的馅饼。说来gameboy的人品实在是太好了，这馅饼别处都不掉，就掉落在他身旁的10米范围内。馅饼如果掉在了地上当然就不能吃了，所以gameboy马上卸下身上的背包去接。但由于小径两侧都不能站人，所以他只能在小径上接。由于gameboy平时老呆在房间里玩游戏，虽然在游戏中是个身手敏捷的高手，但在现实中运动神经特别迟钝，每秒种只有在移动不超过一米的范围内接住坠落的馅饼。现在给这条小径如图标上坐标：
img
为了使问题简化，假设在接下来的一段时间里，馅饼都掉落在0-10这11个位置。开始时gameboy站在5这个位置，因此在第一秒，他只能接到4,5,6这三个位置中其中一个位置上的馅饼。问gameboy最多可能接到多少个馅饼？（假设他的背包可以容纳无穷多个馅饼）

输入格式:

输入数据有多组。每组数据的第一行为以正整数n(0<n<100000)，表示有n个馅饼掉在这条小径上。在结下来的n行中，每行有两个整数x,T(0<T<100000),表示在第T秒有一个馅饼掉在x点上。同一秒钟在同一点上可能掉下多个馅饼。n=0时输入结束。

输出格式:

每一组输入数据对应一行输出。输出一个整数m，表示gameboy最多可能接到m个馅饼。
提示：本题的输入数据量比较大，建议用scanf读入，用cin可能会超时。

输入样例:

1
2
3
4
5
6
7
8
6
5 1
4 1
6 1
7 2
7 2
8 3
0

输出样例:

1
4

例题二、搬寝室

搬寝室是很累的,xhd深有体会.时间追述2006年7月9号,那天xhd迫于无奈要从27号楼搬到3号楼,因为10号要封楼了.看着寝室里的n件物品,xhd开始发呆,因为n是一个小于2000的整数,实在是太多了,于是xhd决定随便搬2k件过去就行了.但还是会很累,因为2k也不小是一个不大于n的整数.幸运的是xhd根据多年的搬东西的经验发现每搬一次的疲劳度是和左右手的物品的重量差的平方成正比(这里补充一句,xhd每次搬两件东西,左手一件右手一件).例如xhd左手拿重量为3的物品,右手拿重量为6的物品,则他搬完这次的疲劳度为(6-3)^2 = 9.现在可怜的xhd希望知道搬完这2*k件物品后的最佳状态是怎样的(也就是最低的疲劳度),请告诉他吧.

输入格式:

每组输入数据有两行,第一行有两个数n,k(2<=2*k<=n<2000).第二行有n个整数分别表示n件物品的重量(重量是一个小于2^15的正整数).

输出格式:

对应每组输入数据,输出数据只有一个表示他的最少的疲劳度,每个一行.

输入样例:

1
2
2 1
1 3

输出样例:

1
4

例题三、最大总和

给定序列 a[1]，a[2]，a[3]……a[n]，你的工作是计算子序列的最大和。例如，给定 （6，-1,5,4，-7），此序列中的最大总和为 6 + （-1） + 5 + 4 = 14。

输入格式:

输入的第一行包含一个整数 T（1<=T<=20），表示测试用例的数量。然后是 T 行，每行以一个数字 N（1<=N<=100000） 开头，然后是 N 个整数（所有整数都在 -1000 到 1000 之间）。

输出格式:

对于每个测试用例，您应该输出两行。第一行是 “Case #：”，# 表示测试用例的编号。第二行包含三个整数，序列中的 Max Sum、子序列的开始位置、子序列的结束位置。如果有多个结果，则输出第一个结果。在两个 case 之间输出一个空行。

输入样例:

1
2
3
2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5

输出样例:

1
2
3
4
5
Case 1:
14 1 4

Case 2:
7 1 6

答案

解法:

前提，若第n个元素前面的最大序列值小于0，果断舍弃前面的值，单独列出做为起始值。

从头开始，用temp不断累加遍历到的元素，不断与max进行比较。若temp<0,则说明后面的值没必要留着前面累赘了，放弃前面，temp=0重新开始记录。

设dp[n]是当前最大序列值数组

则可得动态规划式：dp[n] = dp[n-1] > 0 ? m[n] + dp[n-1] : m[n]。

下面没有用这个式子，但实际想法差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<stdio.h>
#include<stdlib.h>
int main(){
    int n;
    scanf("%d", &n);
    for(int j = 1; j <= n; j++){
        int len;
        scanf("%d", &len);
        int m[100001] = {0};
        for(int i = 1; i <= len; i++){
            scanf("%d", &m[i]);
        }
        int temp = 0;
        int start = 1; 
        int up = 1;
        int end = 1;
        int max = -10000;
        

​    for(int i = 1; i <= len; i++){
​        temp += m[i];
​        if(temp > max){
​            up = start;
​            max = temp;
​            end = i;
​        }if(temp < 0){
​            start = i + 1;
​            temp = 0;
​        }
​    }

​    printf("Case %d:\n%d %d %d\n", j, max, up, end);
​    if(j!=n){
​        printf("\n");
​    }
}

}

6.宽度优先搜索BFS

核心思想：队列

参考链接宽度优先搜索算法（BFS）详解（超级详细讲解，附有大图）-CSDN博客

bfs函数设计

可以参考下面两个例题的bfs函数，函数可以不需要参数值，因为不需要递归，在函数里面主要就是在while循环进行入队出队操作，直至遍历到满足的元素后输出结果+return结束，或者队列为空后再输出结果。

模板一：使用c++的queue对象

queue<结构体对象名> q

q.push(元素对象) 放入对象

q.empty()检测队列是否为空

q.front() 获取队首元素

q.pop() 队首元素出队

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//以下两个是必要的头文件！！！！
#include<queue>
using namespace std;
struct qu{
    int item;
    int step;
};
int main(){
        qu cur = {0, 0};
        queue<qu> q;
        q.push(cur);
        cur = q.front();
        q.pop();
        qu nex;
}

模板二、使用c++的priority_queue对象

priority_queue对象会自动排序，但要求我们自定义的结构体里面有声明相应的排序规则

注意，priority_queue获取队首用的是top(),不是front()

例如

1
2
3
4
5
6
7
8
struct node
{
	int x,y;
	bool operator < (const node & a) const
	{
		return x<a.x;
	}
};

这个node结构体有两个成员，x和y，它的小于规则是x小者小。

就是说若当前x比新来的x要小的话，就return true，进行交换，把大的放在靠近队首的地方。

所以把元素(10,100),(12,60),(14,40),(6,20),(8,20)这五个node加入到队列后，一个个pop()的输出结果是(14,40) (12,60) (10,100) (8,20) (6,80)

参考链接【原创】优先队列 priority_queue 详解-CSDN博客

例题一、胜利大逃亡

7-5 胜利大逃亡

Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.

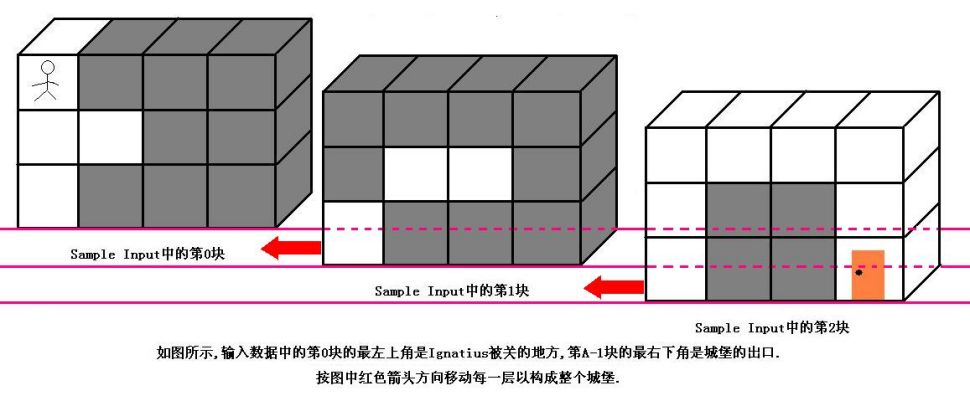
魔王住在一个城堡里,城堡是一个ABC的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个. 现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1.

image.png

输入格式:

输入数据的第一行是一个正整数K,表明测试数据的数量. 每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表城堡的大小和魔王回来的时间. 然后是A块输入数据(先是第0块,然后是第1块,第2块……),每块输入数据有B行,每行有C个正整数,代表迷宫的布局,其中0代表路,1代表墙. (如果对输入描述不清楚,可以参考Sample Input中的迷宫描述,它表示的就是上图中的迷宫)

输出格式:

对于每组测试数据,如果Ignatius能够在魔王回来前离开城堡,那么请输出他最少需要多少分钟,否则输出-1.

输入样例:

1
2
3
4
5
6
7
8
9
10
11
1
3 3 4 20
0 1 1 1
0 0 1 1
0 1 1 1
1 1 1 1
1 0 0 1
0 1 1 1
0 0 0 0
0 1 1 0
0 1 1 0

输出样例:

1
11

答案

注意点：该题是一个三维数组，需要建立三维坐标，以及六个方向数组。

2.bfs函数里，该函数没有传入值，在函数开头需要先把队列里元素全都pop掉，再把初始的node cur = {0, 0, 0, 0}传入到queue<node> q中。

3.函数的结束判定。因为只要能遍历到终点或者当前时间已经超时了，那么一定有输出，所以再输出完之后直接return掉结束函数就可以了。

4.若函数的while循环里，没有最终遍历到终点，那么要记得在while循环外面放一个printf(“-1\n”)语句。

或者在while循环里最后放上这么一段

if(q.empty()){
    printf("-1\n");
    return;
}

总之，核心关键点就是记得拿到结果时，使用return直接结束函数。因为这个老是会忘记┭┮﹏┭┮。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<stdio.h>
#include<stdlib.h>
#include<queue>
#include<string.h>
using namespace std;
int map[51][51][51];
int vis[51][51][51];
int k, a, b, c, t;
struct node{
    int x, y, z;
    int time;
};
queue<node> q;
int dir[6][3] = {{-1, 0, 0}, {1, 0, 0}, {0, -1, 0}, {0, 1, 0}, {0, 0, -1}, {0, 0, 1}};
void bfs(){
    while(!q.empty()){
        q.pop();
    }
    node n = {0, 0, 0, 0};
    q.push(n);
    while(!q.empty()){
        
        node cur = q.front();
        q.pop();
        if(cur.time > t){
            printf("-1\n");
            return;
        }
        if(cur.x == a - 1 && cur.y == b - 1 && cur.z == c -1){
            printf("%d\n", cur.time);
            return;
        }
        node nex;
        for(int i = 0; i < 6; i++){
            int x = cur.x + dir[i][0];
            int y = cur.y + dir[i][1];
            int z = cur.z + dir[i][2];
            if(!vis[x][y][z] && !map[x][y][z] && x >= 0 && x < a && y >= 0 && y < b && z >= 0 && z < c){
                nex = {x, y, z, cur.time+1};
                q.push(nex);
                vis[x][y][z] = 1;
            }
        }
    }
    printf("-1\n");
}
int main(){
    scanf("%d", &k);
    while(k -- >0){
        scanf("%d %d %d %d", &a, &b, &c, &t);
        for(int i = 0; i < a; i++){
            for(int j = 0; j < b; j++){
                for(int p = 0; p < c; p++){
                    scanf("%d", &map[i][j][p]);
                }
            }
        }
        memset(vis, 0, sizeof(vis));
        vis[0][0][0] = 1;
        bfs();
    }
}

例题二、营救

7-4 营救

Angel 被 MOLIGPY 抓住了！他被 Moligpy 关进了监狱。监狱被描述为 N * M （N， M <= 200） 矩阵。监狱里有 WALLs、ROAD 和 GUARDs。Angel 的朋友想救 Angel。他们的任务是：接近 Angel。我们假设 “接近 Angel” 是为了到达 Angel 停留的位置。当网格中有守卫时，我们必须杀死他（或她）才能进入网格。我们假设我们向上、向下、向右、向左移动需要 1 个单位的时间，杀死一个守卫也需要 1 个单位的时间。而且我们足够强大，可以杀死所有的守卫。您必须计算接近 Angel 的最短时间。（当然，我们只能将 UP、DOWN、LEFT 和 RIGHT 移动到边界内的相邻网格。

输入格式:

第一行包含两个整数，分别代表 N 和 M。然后是 N 行，每行有 M 个字符。“.” 代表道路，“a” 代表 Angel，“r” 代表 Angel 的每个朋友。进程到文件末尾。

输出格式:

对于每个测试用例，您的程序应输出一个整数，代表所需的最短时间。如果不存在这样的数字，您应该输出一行，其中包含“可怜的天使必须终生留在监狱中”。

输入样例:

1
2
3
4
5
6
7
8
7 8
#.#####.
#.a#..r.
#..#x...
..#..#.#
#...##..
.#......
........

输出样例:

1
13

答案

解法：

因为这道题里，time的值不是一直+1，还有可能+2,所以，所以用普通的队列不能ac，因为我们要保证队列前面的元素一定要是time最小的，从前到后遍历时，元素的time是非递减的，这样子才能保证遍历到结束点的时候用时最短。故需要在原普通队列的基础上做一点改动就能够ac了。

1.queue<node> q 改为 priority_queue<node> q

2.取队首元素从q.front()改为q.top()。

3.结构体里要内嵌比较函数

1
2
3
4
5
6
7
8
struct node{
	int x, y, time;
    //固定写法，试过了，不能不写const
    bool operator <(const node&other)const{
    	//当前元素的值和其他元素的time比较，若返回true,则交换，即当前元素放到后面，所以就是从小到大排
        return time > other.time;
    }
}

易错点：这道题重新写，让我崩溃的是我x和y的范围没有写全，漏了x >= 0 和 y >= 0，导致一直报段错误，害我找半天错误。

队列会写的话，优先队列只需要改动一点就行了O(∩_∩)O。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<stdio.h>
#include<queue>
#include<stdlib.h>
#include<string.h>
using namespace std;
int n, m, sx, sy;
char map[201][201];
int vis[201][201];
struct node{
    int x, y, time;
    
    bool operator<(const node& other) const {
        return time > other.time;
    }
};
priority_queue<node> q;
int dir[4][2] = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};
void bfs(){
    node st = {sx, sy, 0};
    q.push(st);
    while(!q.empty()){
        node cur = q.top();
        if(map[cur.x][cur.y] == 'r'){
            printf("%d\n", cur.time);
            return;
        }
        q.pop();
        node nex;
        for(int i = 0; i < 4; i++){
            int x = cur.x + dir[i][0];
            int y = cur.y + dir[i][1];
            if(vis[x][y] == 0 && map[x][y] != '#' && x < n && y < m && x >= 0 && y >= 0){
                if(map[x][y] == 'x'){
                    nex = {x, y, cur.time + 2};
                }else{
                    nex = {x, y, cur.time+1};
                }
                vis[x][y] = 1;
                q.push(nex);
            }
        }
    }
    printf("Poor ANGEL has to stay in the prison all his life.\n");
}
int main(){
    while(scanf("%d %d", &n, &m) != EOF){
        q = {};
        for(int i = 0; i < n; i++){
            // getchar();
            scanf("%s", &map[i]);
            for(int j = 0; j < m; j++){
                if(map[i][j] == 'a'){
                    sx = i; 
                    sy = j;
                }
            }
        }
        memset(vis, 0, sizeof(vis));
        vis[sx][sy] = 1;
        bfs();
    }
}

7.深度优先搜索DFS

核心思想：回溯、递归

  1. 为了求得问题的解，先选择某一种可能情况向前探索；
  2. 在探索过程中，一旦发现原来的选择是错误的，就退回一步重新选择，继续向前探索；
  3. 如此反复进行，直至得到解或证明无解。

模板

主要就是设置一个vis数组标记是否访问过。

难点在如何剪枝

参考链接DFS (深度优先搜索) 算法详解 + 模板 + 例题，这一篇就够了_dfs算法-CSDN博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int a[510];   //存储每次选出来的数据
int book[510];   //标记是否被访问
int ans = 0; //记录符合条件的次数

void DFS(int cur){
	if(cur == k){ //k个数已经选完，可以进行输出等相关操作 
		for(int i = 0; i < cur; i++){
			printf("%d ", a[i]);
		} 
		ans++;
		return ;
	}
for(int i = 0; i < n; i++){ //遍历 n个数，并从中选择k个数 
	if(!book[i]){ //若没有被访问 
		book[i] = 1; //标记已被访问 
		a[cur] = i;  //选定本数，并加入数组 
		DFS(cur + 1);  //递归，cur+1 
		book[i] = 0;  //释放，标记为没被访问，方便下次引用 
	}
}

}

例题一、骨头者的诱惑

7-1 骨头的诱惑者

这只小狗在一个古老的迷宫里发现了一根骨头，这让他非常着迷。然而，当他捡起它时，迷宫开始晃动，小狗能感觉到地面在下沉。他意识到那块骨头是一个陷阱，他拼命想走出这个迷宫。迷宫是一个尺寸为 N x M 的矩形。迷宫里有一扇门。一开始，门是关着的，它会在第 T 秒打开一小段时间（不到 1 秒）。因此，这只小狗必须在第 T 秒到达门口。在每一秒内，他可以将一个块移动到上、下、左、右相邻块中的一个。一旦他进入一个方块，这个方块的地面就会开始下沉，并在下一秒消失。他不能在一个区块上停留超过一秒钟，也不能进入一个被访问过的区块。可怜的小狗能活下来吗？请帮助他。

输入格式:

输入由多个测试用例组成。每个测试用例的第一行包含三个整数 N、M 和 T （1 < N， M < 7;0 < T < 50），分别表示迷宫的大小和门打开的时间。接下来的 N 行给出了迷宫布局，每行包含 M 个字符。字符是以下之一： ‘X’：一块墙，小狗不能进入;’S’：小狗的起点;’D’：门;或 ‘.’：一个空块。input 以三个 0 终止。此测试用例不予处理。

输出格式:

对于每个测试用例，如果 doggie 可以存活，则在一行中打印 “YES”，否则打印 “NO”。

输入样例:

1
2
3
4
5
6
7
8
9
10
4 4 5
S.X.
..X.
..XD
....
3 4 5
S.X.
..X.
...D
0 0 0

输出样例:

1
2
NO
YES

答案

解法：

dfs和剪枝

1.dfs()，以当前元素的位置和时间作为参数

2.剪枝。当目前时间减去最短距离所需时间时的剩余时间小于0，或者等于奇数时，那么该点一定走不到终点，直接return。

问题：该代码读取map各个位置的元素时不能使用getchar()加scanf(),cin或者直接scanf(“%s”)就可以，也不知道为什么。我自己重新写时出一堆问题，明明和原代码差不多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<iostream>
using namespace std;
int n, m, t, nt;
int ex, ey;
char map[10][10];
int flag = 0;
int dir[4][2] = {{0,1}, {1, 0}, {-1, 0}, {0, -1}};
void dfs(int x, int y, int cnt){
    if(x >= n || x < 0 || y >= m || y < 0){
        return;
    }
    if(x == ex && y == ey && cnt == t){
        flag = 1;
        return;
    }
    if(flag){
        return;
    }
    int temp = t - cnt - fabs(x - ex) - fabs(y - ey);
    if(temp < 0 || temp % 2 == 1){
        return;
    }
    for(int i = 0; i < 4; i++){
        if(map[x + dir[i][0]][y + dir[i][1]] != 'X'){
            map[x + dir[i][0]][y + dir[i][1]] = 'X';
            dfs(x + dir[i][0], y + dir[i][1], cnt+1);
            if(flag){
                return;
            }
            map[x + dir[i][0]][y + dir[i][1]] = '.';
        }
    }
    return;
}
int main(){
    int sx, sy;
    while(scanf("%d%d%d",&n,&m,&t)&&(m+n+t)){
        flag = 0;
        for(int i = 0; i < n; i++){
        //scanf("%s", &map[i]);
            for(int j = 0; j < m; j++){
                cin>>map[i][j];
                if(map[i][j] == 'S'){
                    sx = i;
                    sy = j;
                }
                else if(map[i][j] == 'D'){
                    ex = i; 
                    ey = j;
                }
            }
        }
        map[sx][sy] = 'X';
        dfs(sx, sy, 0);
        if(flag){
            printf("YES\n");
        }else{
            printf("NO\n");
        }
    }
    return 0;
}

例题二、FatMouse 和奶酪

7-7 FatMouse 和奶酪

FatMouse 在一个城市储存了一些奶酪。城市可以看作是维度 n 的方形网格：每个网格位置都标记为 （p，q），其中 0 <= p < n 和 0 <= q < n。在每个网格位置，Fatmouse 都在一个洞中隐藏了 0 到 100 块奶酪。现在他要享受他最喜欢的食物了。FatMouse 首先站在位置 （0,0）。他吃掉了自己站着的奶酪，然后水平或垂直地跑到另一个地方。问题是有一只名叫 Top Killer 的超级猫坐在他的洞附近，所以每次他最多可以跑 k 个位置进入洞中，然后被 Top Killer 抓住。更糟糕的是 – 在一个地方吃完奶酪后，FatMouse 变得更胖了。因此，为了获得足够的能量进行下一次跑步，他必须跑到一个比当前洞的奶酪块更多的地方。给定 n、k 和每个网格位置的奶酪块数，计算 FatMouse 在无法移动之前可以吃的最大奶酪量。

输入格式:

有几个测试用例。每个测试用例由一行组成，其中包含两个介于 1 和 100 之间的整数：n 行和 k n 行，每行有 n 个数字：第一行包含位置 （0,0） （0,1） 的奶酪块数……（0，n-1）;下一行包含位置 （1,0）、（1,1）、…（1，n-1） 等。input 以一对 -1 结尾。

输出格式:

对于每个测试用例，在一行中输出单个整数，给出收集的奶酪块数。

输入样例:

1
2
3
4
5
3 1
1 2 5
10 11 6
12 12 7
-1 -1

输出样例:

1
37

答案:

解法：dfs+dp

这道题需要注意的是，由于要计算收集的奶酪的最大值，所以我们不能只单纯进行dfs，而应该在dfs过程中运用dp思想，把当前位置可以拿到的最大奶酪数记录到dp数组里。而且由于只能走比自己当前位置大的数的方向，所以没有必要再用vis数组记录当前位置是否被遍历过。

剪枝:

若dp数组一开始就赋予了和map数组一样的值，那么进行dfs时，遍历到的位置最大值可能要求好多次。

从结果推到起点来看，如果我们在dfs中开始先判断dp是否有值，若有，若没有，那么再把同样位置的map值赋给dp当初始值进行最大值搜索，因为这样做，如果从别的位置又遍历到当前位置时，不需要再进行dfs下去，直接return该值即可，因为之前已经dfs过，把当前位置的最大值给记录到了。总之就是当前dp进行dfs后就已经获取最大值了，只是借用dp不为0来进行直接返回。换用其他标记数组也可以达到同样效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int max(int a, int b){
    if(a > b)
        return a;
    else
        return b;
}
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int n, k;
int map[110][110];
int dp[110][110];
int res;
int dfs(int x, int y){
    if(dp[x][y] != 0){
        return dp[x][y];
    }
    dp[x][y] = map[x][y];
    int tx, ty, flag = 0;
    for(int j = 1; j <= k; j++){
        for(int i = 0; i < 4; i++){
            tx = dir[i][0] * j + x;
            ty = dir[i][1] * j + y;
            if(tx >= 0 && ty >= 0 && tx < n && tx < n){
                if(map[tx][ty] > map[x][y]){
                    dp[x][y] = max(map[x][y] + dfs(tx, ty), dp[x][y]);
                }
            }
            
        }
        
    }
    return dp[x][y];
}


int main(){
    while(scanf("%d %d", &n, &k) ){
        if(n == -1 && k == -1){
            break;
        }
        // memset(map, 0, sizeof(map));
        for(int i = 0; i < n; i++){
            for(int j = 0; j <  n; j++){
                scanf("%d", &map[i][j]);
            }
        }
        memset(dp, 0, sizeof(dp));

        res = dfs(0, 0);
        printf("%d\n", res);
    }
}

8.并查集

核心思想：找父亲findp(), 合并merge()

1.给每个元素都先把它们自己定义为父亲。

2.查找目标元素父亲时，使用while循环，直至遍历的当前元素的父亲等于当前元素，此时当前元素即为目标元素的父类。

3.合并时要注意，合并的是当前两个元素的父亲，即先findp(x)和findp(y)，把x和y的父亲先找到，再给y的父亲的父亲设置为x的父亲。而不是直接f[x] = y!!!!。

优化：

查找目标元素父亲时，顺便把找父亲时遍历的其他元素的f[n]也都直接设置为父亲，这样子可以有效减少之后找父亲的循环次数。例如

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int findp(int x){
    int r = x;
    //找到最终的父亲
    while(f[r] != r){
        r = f[r];
    }
    //给当前元素的f直接设置为父亲的值
    //i存储当前元素，j存储当前元素的f
    int i=x,j;
    while(f[i]!=r)
    {
        j=f[i];
        f[i]=r;
        i=j;
    }
    return r;
}

模板

1.findp函数如上面的优化写即可

2.merge函数

注意：merge函数有两种写法，一个是在merge里找父亲元素，一个是在调用merge函数之前把父亲找好了再传值

1
2
3
4
5
6
7
8
9
10
//写法1
void merge(int x, int y){
    int xp = findp(x);
    int yp = findp(y);
    f[yp] = xp;
}
//写法2
void merge(int x, int y){
	f[y] = x;
}

例题一、畅通工程再续

7-3 畅通工程再续

全屏浏览切换布局

作者 刘春英

单位 杭州电子科技大学

相信大家都听说一个“百岛湖”的地方吧，百岛湖的居民生活在不同的小岛中，当他们想去其他的小岛时都要通过划小船来实现。现在政府决定大力发展百岛湖，发展首先要解决的问题当然是交通问题，政府决定实现百岛湖的全畅通！经过考察小组RPRush对百岛湖的情况充分了解后，决定在符合条件的小岛间建上桥，所谓符合条件，就是2个小岛之间的距离不能小于10米，也不能大于1000米。当然，为了节省资金，只要求实现任意2个小岛之间有路通即可。其中桥的价格为 100元/米。

输入格式:

输入包括多组数据。输入首先包括一个整数T(T <= 200)，代表有T组数据。
每组数据首先是一个整数C(C <= 100),代表小岛的个数，接下来是C组坐标，代表每个小岛的坐标，这些坐标都是 0 <= x, y <= 1000的整数。

输出格式:

每组输入数据输出一行，代表建桥的最小花费，结果保留一位小数。如果无法实现工程以达到全部畅通，输出”oh!”.

输入样例:

1
2
3
4
5
6
7
8
2
2
10 10
20 20
3
1 1
2 2
1000 1000

输出样例:

1
2
1414.2
oh!

答案

解法

贪心+并查集

1.该题使用并查集之前，需要自己在读完所有岛屿信息后，根据条件筛选出两两对应的不同岛屿，把他们的编号和距离存放到结构体数组node中。由于两个for循环遍历完，所以结构体node数组开辟的大小应该是c*(c-1)/2。之后使用qsort函数排序后进行并查集操作。

易错点

node数组的大小不等于岛的个数c，而是等于c(c-1)/2*，这点很重要，否则一直报段错误。还有，qsort函数里面排序数量也是c*(c-1),这些都是极易忽视的易错点啊(╯°□°）╯︵ ┻━┻。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
int t, c;
struct node{
    int a, b;
    double dis;
}node[10000];
int land[111][2], f[111], vis[101];
int cmp(const void * a, const void * b){
    struct node x = *(struct node*)a;
    struct node y = *(struct node*)b;
    if(x.dis - y.dis > 0){
        return 1;
    }
    return -1;
}
int findp(int x){
    int r = x;
    while(f[r] != r){
        r = f[r];
    }
    int a = x, b;
    while(f[a] != r){
        b = f[a];
        f[a] = r;
        a = b;
    }
    return r;
}
void merge(int a, int b){
    f[b] = a;
}
int main(){
    scanf("%d", &t);
    while(t--){
        scanf("%d", &c);
        for(int i = 0; i < c; i++){
            scanf("%d %d", &land[i][0], &land[i][1]);
        }
        double dis = 0;
        int index = 0;
        for(int i = 0; i < c-1; i ++){
            for(int j = i + 1; j < c; j++){
                dis = sqrt(pow(land[j][0] - land[i][0], 2)+pow(land[j][1]-land[i][1], 2));
                if(dis >= 10 && dis <= 1000){
                    node[index].a = i;
                    node[index].b = j;
                    node[index].dis = dis;
                    index++;
                }
            }
        }
        for(int i = 0; i < c; i++){
            f[i] = i;
        }
        double sum = 0;
        int num = 0;
        qsort(node, c*(c-1)/2, sizeof(struct node), cmp);
        for(int i = 0; i < index; i++){
            int fx = findp(node[i].a);
            int fy = findp(node[i].b);
            if(fx != fy){
                merge(fx, fy);
                sum += node[i].dis;
                num++;
            }
        }
        if(num == c - 1)
            printf("%.1lf\n", sum*100);
        else
            printf("oh!\n");
    }
}

例题二、Is It A Tree

7-6 Is It A Tree?

全屏浏览切换布局

作者 刘春英

单位 杭州电子科技大学

A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.

Every node except the root has exactly one edge pointing to it.

There is a unique sequence of directed edges from the root to each node.

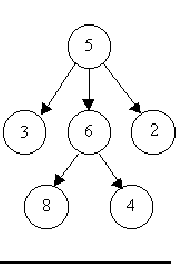
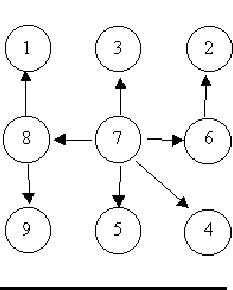
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
image.pngimage.pngimage.png

In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.

输入格式:

The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.

输出格式:

For each test case display the line Case k is a tree." or the line Case k is not a tree.”, where k corresponds to the test case number (they are sequentially numbered starting with 1).

输入样例:

1
2
3
4
5
6
7
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1

输出样例:

1
2
3
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.

答案

解法

1.一个节点有两个父节点时，这就不是一个树了。所以在合并前，应先判断b是否已经有父节点了。

2.用一个vis数组来记录节点是否存在，若存在，再根据其是否等于父节点（即该节点是否是根），给sum+1, 若最后sum==1,则是树，否则不是树。

3.空集合是树，即输入为 0 0 的情况。因此需要额外判断。

易错点

气死我了，输出样例最后句子有个小数点，但我没注意，结果一直反复查看代码哪里出错了，(╯▔皿▔)╯。另外，该题不能用两个while循环来读取数据，会一直超时。也不知道啥原因。所以只能用一个while循环来写，若遍历到了0 0，则调用isAtree()函数判断是否是树，再用initial()函数重置数据。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int f[10005], vis[10005];
int flag = 1,index = 1;
int findp(int a){
    int r = a;
    while(r != f[r]){
        r = f[r];
    }
    int x =a, y;
    while(f[x] != r){
        y = f[x];
        f[x] = r;
        x = y;
    }
    return r;
}
void merge(int x, int y){
    f[y] = x;
}
void initial(){
    for(int i = 0; i < 10005; i++){
        f[i] = i;
    }
    memset(vis, 0, sizeof(vis));
    flag = 1;
}
void isAtree(){
    int sum = 0;
    if(flag == 0){
        printf("Case %d is not a tree.\n", index++);
        return;
    }
    int ok = 0;
    for(int i = 0; i < 10005; i++){
        if(vis[i]){
            ok = 1;
            if(f[i] == i){
                sum += 1;
            }
        }
    }
    
    if(sum == 1 || !ok){
        printf("Case %d is a tree.\n", index++);
    }else{
        printf("Case %d is not a tree.\n", index++);
    }
}
int main(){
    int a, b;
    initial();
    while(scanf("%d %d", &a, &b) != EOF){
        if(a == -1 && b == -1){
            break;
        }
        if(a == 0 && b == 0){
            isAtree();
            initial();
            continue;
        }
        else{
            vis[a] = 1;
            vis[b] = 1;
            if(f[b] != b || a == b){
                flag = 0;
            }
            int fa = findp(a);
            int fb = findp(b);
            if(fa != fb){
                merge(fa, fb);
            }
        }
    }
}