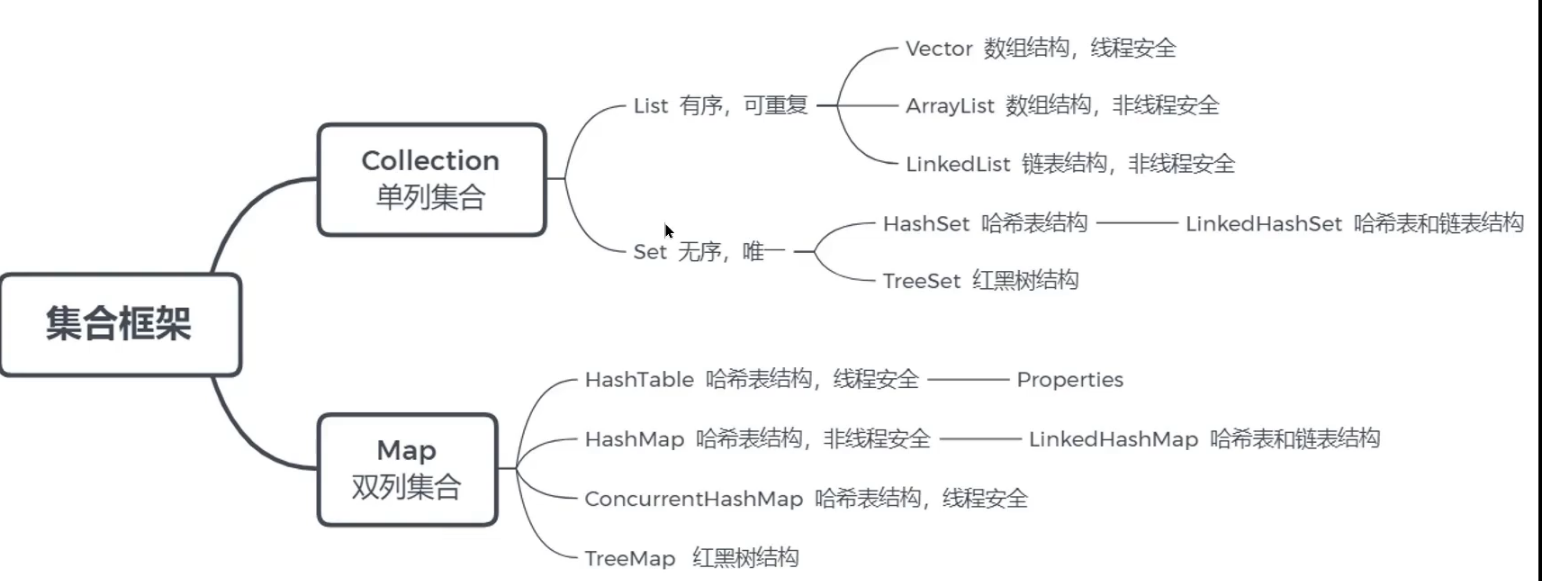
一、内容概览

二、算法复杂度

要想深入学习集合的底层原理，就要先对复杂度的概念有个清晰的认知。

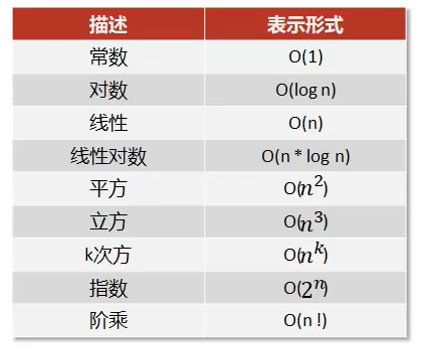
（1）时间复杂度

时间复杂度表示了算法的执行时间与数据规模n之间的增长关系。

常见的时间复杂度：O(1)、O(n)、O(n^2)、O(logn)

速记口诀：常对幂指阶

（2）空间复杂度

空间复杂度表示算法占用的额外存储空间和数据规模n之间的增长关系。

三、List

1.ArrayList

(1)数据结构

ArrayList底层使用数组来存储数据的。数组是一种用连续的内存空间存储相同数据类型的线性数据结构。

(2)基础问题

1.数组下标为什么从0开始

这就涉及到了数组元素的内存地址的计算问题了。

寻址公式：baseAddress + i * dataType，计算下标的内存地址速率高。

人话：基地址 + 索引下标 * 元素类型占用的空间大小

如果索引是从1开始，那么寻址公式就需要对（i-1），对于cpu来说，相当于多了一个减法指令。

2.查找的时间复杂度

随机(通过下标)查找的时间复杂度是O(1)
查找未知下标的元素的时间复杂度是O(n)
如果未知下标，但数组是排好序的，那么利用二分查找的时间复杂度是O(logn)

3.插入和删除的时间复杂度

插入和删除的时间复杂度，在尾插和尾删的情况下是O(1)。这种情况下不需要挪动数组的其他元素。但它们的**平均复杂度均为O(n)**。

(3)源码分析

分析源码主要从三方面进行分析：成员变量、构造函数和关键方法

成员变量

//默认容量大小
private static final int DEFAULT_CAPACITY = 10;
//指定容量为0时的使用到的空实例
private static final Object[] EMPTY_ELEMENTDATA = {};
//使用默认的无参构造函数时创建的空实例
private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};
//存放元素的数组对象
transient Object[] elementData; 
//数组元素数量
private int size;

区分两个空实例

关键看grow方法

private Object[] grow(int minCapacity) {
    //获取当前数组长度
    int oldCapacity = elementData.length;
    //如果数组长度>0 又或者该ArrayList是通过有参构造器传入0值创建的一个暂未添加任何元素的空实例
    if (oldCapacity > 0 || elementData != DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
        //容量扩充为1.5倍
        int newCapacity = ArraysSupport.newLength(oldCapacity,
                minCapacity - oldCapacity, /* minimum growth */
                oldCapacity >> 1           /* preferred growth */);
        //拷贝旧数组元素至新容量数组
        return elementData = Arrays.copyOf(elementData, newCapacity);
    } else {
        //对于使用无参构造函数创建的ArrayList，在数组长度为0时，容量扩充为10
        return elementData = new Object[Math.max(DEFAULT_CAPACITY, minCapacity)];
    }
}
//获取1.5倍容量大小
public static int newLength(int oldLength, int minGrowth, int prefGrowth) {
    // preconditions not checked because of inlining
    // assert oldLength >= 0
    // assert minGrowth > 0
	//数组初始容量为0时，容量扩容为1，就是因为这里判断了容量差值和扩充容量的最大值
    int prefLength = oldLength + Math.max(minGrowth, prefGrowth); // might overflow
    if (0 < prefLength && prefLength <= SOFT_MAX_ARRAY_LENGTH) {
        return prefLength;
    } else {
        // put code cold in a separate method
        return hugeLength(oldLength, minGrowth);
    }
}

总之，两个空实例主要区别就是在数组长度为0时，会使用的不同的扩容策略。使用无参构造器创建的对象，在第一次add元素时，容量直接扩充为10。对于使用有参构造函数创建的对象，扩容策略直接就是使用1.5倍扩容，即使传入的参数是0，也是1.5倍方式扩容为1。

构造函数

//无参构造函数
public ArrayList() {
    //赋值 无参构造函数所以使用的空实例
    this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA;
}

//有参构造函数
public ArrayList(int initialCapacity) {
    if (initialCapacity > 0) {
        this.elementData = new Object[initialCapacity];
    } else if (initialCapacity == 0) {
        //赋值 有参构造函数传入容量为0时的空实例
        this.elementData = EMPTY_ELEMENTDATA;
    } else {
        throw new IllegalArgumentException("Illegal Capacity: "+
                                           initialCapacity);
    }
}

关键方法

//添加元素
public boolean add(E e) {
    modCount++; //记录集合的修改次数，用于迭代过程中判断是否发生了并发修改
    add(e, elementData, size);
    return true;
}

private void add(E e, Object[] elementData, int s) {
    if (s == elementData.length)
        elementData = grow();
    elementData[s] = e;
    size = s + 1;
}
//grow方法详解在成员变量处

(4)面试题

ArrayList底层的实现原理是什么

ArrayList底层是用动态数组实现的
ArrayList使用无参构造函数创建时，初始容量为0，当第一次添加元素时，容量扩充为10。
而当使用有参构造函数创建时，初始容量为传入的容量值。
无参第一次扩容之后和有参每次扩容都是扩容为原来大小的1.5倍。
ArrayList在添加元素时

会确保数组已使用长度加1之后足够存放下一个数据。

如果已使用长度加1大于当前数组容量，则调用grow()方法进行1.5倍扩容。

添加成功之后就会返回布尔值。

ArrayList list = new ArrayList(10)中list会扩容几次

扩容0次，看有参构造函数的具体实现就知道了，是直接创建一个对应容量的数组进行赋值，根本没进行扩容。

如何实现数组和List之间的转换

public static void main(String[] args) {
    //数组转list,使用Arrays工具类的asList方法
    Integer[] arr = new Integer[10];
    int[] a = new int[10];
    List<Integer> list1 = Arrays.asList(arr);
    List<int[]> list2 = Arrays.asList(a); //因为int类型不属于引用类型，所以把整个int数组作为元素类型了
	//list转数组,使用toArray方法
    ArrayList<Integer> list = new ArrayList<>();
    Object[] array = list.toArray(); //无参，返回一个Object数组
    Integer[] array1 = list.toArray(new Integer[10]); //有参，返回传入的数组对象
}

追问，用Arrays.asList转List后，如果修改了数组内容，list受影响吗？

受影响，asList是把原数组作为List的动态数组，也就是List的数组引用的是原来的数组

public static <T> List<T> asList(T... a) {
    return new ArrayList<>(a);
}
ArrayList(E[] array) {
	a = Objects.requireNonNull(array); //判断数组是否为null，不为null则直接引用，为null则跑异常
}

List用toArray转数组之后，如果修改了list内容，数组受影响吗？

不受影响，因为toArray其实是把list中的数组进行了拷贝并返回的。

public Object[] toArray() {
    //返回一个相同容量的拷贝数组
	return Arrays.copyOf(elementData, size);
}

public <T> T[] toArray(T[] a) {
    if (a.length < size)
        //把list中的数组元素拷贝到传入的数组对象上
        return (T[]) Arrays.copyOf(elementData, size, a.getClass());
    System.arraycopy(elementData, 0, a, 0, size);
    if (a.length > size)
        a[size] = null;
    return a;
}

2.LinkedList

(1)数据结构

LinkedList底层使用的是双向链表的数据结构。

对于传入LinkedList的每个元素，都会封装到Node对象上。Node对象包含了存储元素和前后驱指针。

private static class Node<E> {
    E item;
    Node<E> next;
    Node<E> prev;
    Node(Node<E> prev, E element, Node<E> next) {
        this.item = element;
        this.next = next;
        this.prev = prev;
    }
}

(2)源码分析

成员变量

1
2
3

transient Node<E> first; //头节点

transient Node<E> last; //尾节点

LinkedList底层就是基于节点的操作，没什么好分析的，所以就先不写了

(3)面试题

ArrayList跟LinkedList的区别是什么

1.底层数据结构

ArrayList使用动态数组，LinkedList使用双向链表

2.操作效率

增删改查的时间复杂度角度

对于查询来说，ArrayList可以使用下标来查询，时间复杂度是O(1)。当未知下标时，ArrayList和LinkedList一样都是O(n)。

对于增删来说，两者基于头尾时间复杂度都是O(1)。其他情况，由于ArrayList增删元素需要挪动数组，Linked需要顺序遍历，所以两者一样都是O(n)。

3.占用空间

LinkedList占用空间更大，因为每个元素都存储了前后驱节点指针。

4.线程是否安全

两者线程都不安全。

如果需要保证线程安全，有两种方案：

第一种，在方法内使用来直接避免，因为局部变量是线程安全的。

第二种，使用线程安全的ArrayList和LinkedList。即使用Collections工具类的synchronizedList方法。

1 2	List<Object> objects = Collections.synchronizedList(new ArrayList<>()); List<Object> objects1 = Collections.synchronizedList(new LinkedList<>());

synchronizedList方法底层就是给方法添加synchronized悲观锁来保证的

@SuppressWarnings("serial") // Conditionally serializable
final List<E> list; //传入的list对象
final Object mutex;     // Object on which to synchronize
public E get(int index) {
    synchronized (mutex) {return list.get(index);}
}
public E set(int index, E element) {
    synchronized (mutex) {return list.set(index, element);}
}
public void add(int index, E element) {
    synchronized (mutex) {list.add(index, element);}
}

四、Map

1.HashMap

(1)数据结构

二叉搜索树

又名二叉查找树、有序二叉树或者排序二叉树。

特点

树的任意一个节点，其左节点的值小于当前节点值，右节点的值大于当前节点值，没有键值（节点值）相同的节点

时间复杂度分析

**通常情况下时间复杂度为O(logn)，但最坏情况就是，如果二叉搜索树退化成了链表，也就是左右子树极度不平衡的情况下，时间复杂度为O(n)**。

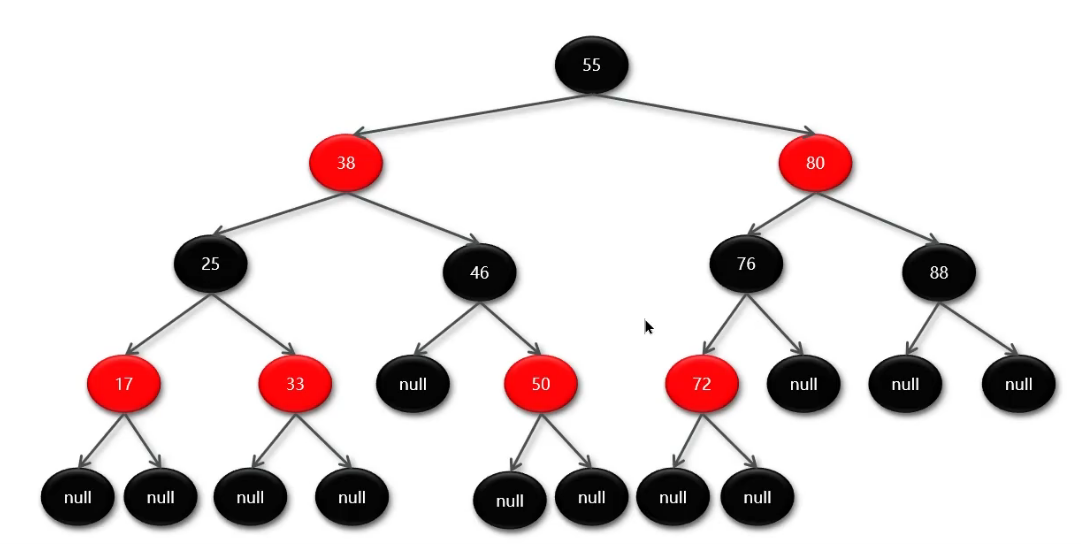
红黑树

也叫自平衡的二叉搜索树。

特点

节点要么是红色，要么是黑色
根节点是黑色
叶子节点是黑色的空节点
红色节点的子节点都是黑色
从任一节点到它的后代叶子节点的所有路径上，黑色节点数目相同

这5个特点本质上就是用来保证二叉树的平衡。

当规则被打破时，通过颜色翻转和左旋右旋来恢复规则。

散列表

散列表，又名哈希表。是根据键（key）直接访问在内存存储位置值（value）的数据结构。由数组演化而来，利用率数组支持按照下标随机访问数据的特点。

散列冲突

又名哈希冲突，指多个key映射到同一个数组的下标位置的情况。

解决方法：链表法。

数组的每个下标位置称为桶或者槽。每个桶会对应一个链表。hash冲突后的元素都放到相同槽位对应的链表中或者红黑树中。

(2)源码分析

成员变量

//默认初始化的数组容量
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; 
//最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
//默认的负载因子大小
static final float DEFAULT_LOAD_FACTOR = 0.75f;
//转化为红黑树时的所需的链表长度阈值
static final int TREEIFY_THRESHOLD = 8;
//红黑树退化为链表时的节点数阈值
static final int UNTREEIFY_THRESHOLD = 6;
//转化为红黑树时的所需的数组容量阈值
static final int MIN_TREEIFY_CAPACITY = 64;
//节点对象
static class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;

    Node(int hash, K key, V value, Node<K,V> next) {
        this.hash = hash;
        this.key = key;
        this.value = value;
        this.next = next;
    }
	//其他方法略
}
//node类型的数组，存放链表或者hash表的头节点
transient Node<K,V>[] table;
//缓存entrySet()方法的放回值
transient Set<Map.Entry<K,V>> entrySet;
//键值对数量
transient int size;
//修改次数
transient int modCount;
//扩容阈值
int threshold;
//负载因子
final float loadFactor;

构造函数

Hashmap的数组是懒加载，只有第一次put时才会初始化。

public HashMap() {
    //使用默认的负载因子
    this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
public HashMap(int initialCapacity, float loadFactor) {
    if (initialCapacity < 0)
        throw new IllegalArgumentException("Illegal initial capacity: " +
                                           initialCapacity);
    if (initialCapacity > MAXIMUM_CAPACITY)
        initialCapacity = MAXIMUM_CAPACITY; //容量不能超过最大值
    if (loadFactor <= 0 || Float.isNaN(loadFactor)) //负载因子不能为空或者小于等于0
        throw new IllegalArgumentException("Illegal load factor: " +
                                           loadFactor);
    this.loadFactor = loadFactor; 
    this.threshold = tableSizeFor(initialCapacity); 
}
//计算大于等于给定容量大小的最小的2的幂次，确保数组大小为2的幂次
static final int tableSizeFor(int cap) {
    int n = -1 >>> Integer.numberOfLeadingZeros(cap - 1);
    return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

关键方法

put方法

public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}
//onlyIfAbsent:是否仅在键不存在的情况下才插入值。evict:控制是否启用驱逐机制
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    //第一次put时，数组初始化。
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    //将（数组容量-1）和key的hash值进行与运算得到下标，如果下标对应的元素为null,则直接添加该节点
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    //否则进行key判断后,进行value替换或者添加节点
    else {
        Node<K,V> e; K k;
        //key相同，则直接进行value替换
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        //如果首元素节点p是红黑树节点，则走红黑树添加节点方法
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        //走链表
        else {
            for (int binCount = 0; ; ++binCount) {
                //获取当前节点的下一个节点，并进行判断
                if ((e = p.next) == null) {
                    //e为null值，添加至链表尾部
                    p.next = newNode(hash, key, value, null);
                    //若添加节点前，链表元素个数已经大于等于7了，则试着转化为红黑树
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash); 
                    break;
                }
                //key相同，进行value替换
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;
    //大于扩容阈值，就进行扩容
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}
final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    //数组长度大于等于64阈值时，才可以转化为红黑树
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        resize();  //扩容
    //计算要转化为红黑树的链表，在数组中的下标
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        TreeNode<K,V> hd = null, tl = null;
        //构建双向链表
        do {
            TreeNode<K,V> p = replacementTreeNode(e, null);
            if (tl == null)
                hd = p;
            else {
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        if ((tab[index] = hd) != null)
            //通过头节点进行树化，构建红黑树
            hd.treeify(tab);
    }
}
//计算哈希值
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); //右移16位后进行&运算，扰动算法，让hash值分布更均匀
}

resize方法

final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        //容量安全校验
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    //由带初始容量的构造函数可知，初始化容量是存放在了threadshold，所以这里才把threadshold赋值给了newCap
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    //无初始容量构造函数创建的对象，使用默认的初始化容量大小
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    //计算新的扩容阈值
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    //设置新的扩容阈值
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    if (oldTab != null) {
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                //处理每个桶中的元素
                oldTab[j] = null;
                //没有hash冲突，则计算新的索引位置后直接添加到新的数组中
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;
                //如果是红黑树，则走红黑树添加
                else if (e instanceof TreeNode)
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                //否则，是链表
                else { // preserve order
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do {
                        next = e.next;
                        //为0，则将当前节点添加到loHead所在的链表中
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        //为1，将当前节点添加到hiHead所在的链表中
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    // loHead停留在原始位置
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    // hiHead移动到原始位置 + oldCap的位置上
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

(3)面试题

说下HaspMap的实现原理

HashMap底层使用的是hash表数据结构，就是数组+链表/红黑树。

添加数据时，会通过计算key的hash值来确定元素在数组中的下标。当链表或者红黑树的中的元素key和当前key相同的话，就会进行value替换，不同的话，就会存入链表或者红黑树中。

HashMap的jdk1.7和jdk1.8有什么区别

JDK1.8之前采用的是拉链法，就是数组+链表。

JDK1.8及以后使用的是数组+链表/红黑树的形式。当链表长度大于8且数组长度大于64，就会把链表转化为红黑树。当扩容时，如果红黑树的结构个数小于等于临界值6时，就会退化成链表。

HashMap的put方法的具体流程

HashMap的table数组是懒加载，所以第一次put才会进行初始化。
判断键值对数组table是否为空或为null,执行resize()进行扩容（初始化）。
根据键值key计算hash值得到数组索引。
判断table[i]==null，条件成立，直接新建节点添加。

如果table[i]!=null,则进行判断

先判断table[i]的首个元素是否和key一样，如果相同则直接覆盖value

否则再判断节点类型是否是TreeNode,如果是，则说明是红黑树，那么就在红黑树中进行节点判断和添加。

否则就是链表，那么遍历整个链表，有key相同的节点，就进行value替换，不然就尾插。尾插完成之后，会判断是否需要转化为红黑树，先进行链表节点个数的阈值判断，再进行数组长度的阈值判断，决定是否将该链表转化为红黑树。

5.插入完成之后，会判断当前节点个数是否大于扩容阈值，如果大于就进行扩容。

HashMap的resize方法的具体流程

HashMap的数组是懒加载模式，在第一次put时，就会调用resize方法来进行数组初始化，如果在构造HashMap时，传入了初始化大小，就初始化为大于等于大小的2的幂次，否则使用默认初始化大小16对数组进行初始化。

以后每次扩容都是在容量到达了扩容阈值（数组长度*0.75）时进行扩容，每次扩容的时候，都是扩容前容量的2倍。

扩容之后，会创建一个新的数组，需要把老数组中的数据挪动到新的数组中。

没有hash冲突的节点，则直接使用e.hash &(newCap-1)计算新数组的索引位置。

如果是红黑树，则走红黑树的添加。

如果是链表，则需要遍历链表，判断链表中的每个元素的hash & oldCap的值是否为0，若为0，则该位置的元素要么停留在原始位置，要么移动到原始位置+增加的数组大小的这个位置上。

HashMap的寻址算法

计算对象的HashCode()

再调用hash方法进行二次哈希，就是hashcode值右移16位再进行异或运算，让哈希分布更为均匀

最后通过（capacity-1）& hash 得到索引

为什么HashMap数组的长度一定是2的次幂

因为这样子计算索引的效率更高，如果是2的n次幂，可以使用位与运算代替取模

扩容时，重新计算索引效率更高，hash&oldCap == 0 的元素留在原来位置，否则新位置=旧位置 + oldCap

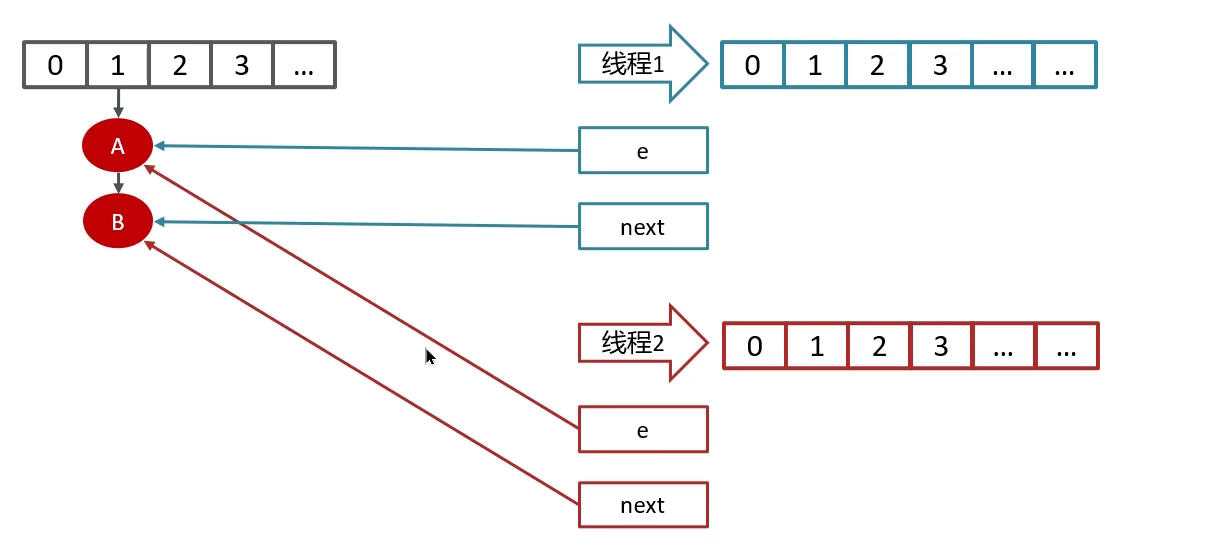
HashMap在jdk1.7情况下的多线程死循环问题

jdk1.7的hashMap在数组进行扩容的时候，因为链表是采用头插法，如果有多个线程对hashMap进行扩容，在数据迁移过程中有可能导致死循环问题。

比如说，有两个线程1和2

线程1，读取到hashmap的数据，在准备扩容时，

线程2介入，线程2先进行了扩容，对数据进行了迁移，由于采用头插法，比如原来链表的顺序是A->B，扩容之后的顺序是B->A，线程2执行结束。

此时，线程1再去扩容就会出现死循环问题。

线程1先将A移入新链表，然后B又插入到链表头。由于线程2的介入，导致B的next不是null,而是A，导致A又重新插入到链表头，从而出现了A -> B -> A的死循环引用。

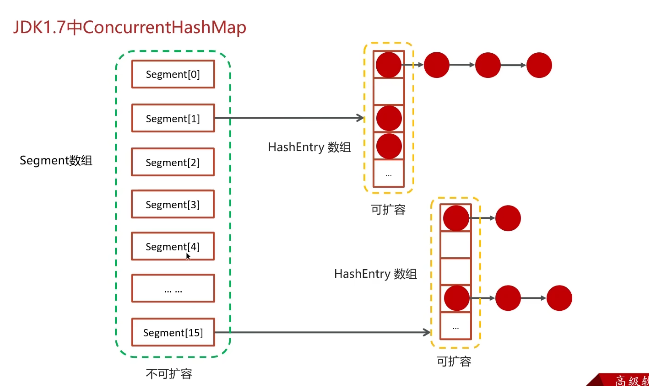
2.ConcurrentHashMap

(1)数据结构

ConcurrentHashMap在JDK1.7及以前采用分段数组+链表实现。

分段数组叫做Segment数组，它是默认固定长度为16的数组，也可以指定。每个Segment元素（继承了Reentrantlock）内部维护了一个数组，叫做HashEntry数组，但这个数组可扩容，且会通过链表连接相同索引下的元素。当多个线程往同个Segment元素维护的数组添加数据时，需要通过ReentrantLock的tryLock方式获取当前元素的锁，只有获取到锁的线程才可以往该节点指向的数组中添加元素，其他线程会通过CAS进行自旋获取。

JDK1.8及以后，采用跟HashMap一样的数据结构，数组+链表/红黑树。去掉Segment数组这个臃肿的设计。

(2)源码分析

put方法

public V put(K key, V value) {
    return putVal(key, value, false);
}

final V putVal(K key, V value, boolean onlyIfAbsent) {
    if (key == null || value == null) throw new NullPointerException();
    int hash = spread(key.hashCode());
    int binCount = 0;
    for (Node<K,V>[] tab = table;;) {
        Node<K,V> f; int n, i, fh; K fk; V fv;
        if (tab == null || (n = tab.length) == 0)
            tab = initTable();
        else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
            //数组该位置=null,通过CAS来添加元素
            if (casTabAt(tab, i, null, new Node<K,V>(hash, key, value)))
                break;                   // no lock when adding to empty bin
        }
        else if ((fh = f.hash) == MOVED)
            tab = helpTransfer(tab, f);
        //为了实现putIfAbsent()方法而引入的，如果onlyIfAbsent为true,那么当首节点key相同，且对应val不为null时，返回旧值，不进行添加
        else if (onlyIfAbsent // check first node without acquiring lock
                 && fh == hash
                 && ((fk = f.key) == key || (fk != null && key.equals(fk)))
                 && (fv = f.val) != null)
            return fv;
        else {
            V oldVal = null;
            //使用synchronized锁住首节点
            synchronized (f) {
                if (tabAt(tab, i) == f) {
                    if (fh >= 0) {
                        binCount = 1;
                        for (Node<K,V> e = f;; ++binCount) {
                            K ek;
                            if (e.hash == hash &&
                                ((ek = e.key) == key ||
                                 (ek != null && key.equals(ek)))) {
                                oldVal = e.val;
                                //如果onlyIfAbsent==false，才允许替换
                                if (!onlyIfAbsent)
                                    e.val = value;
                                break;
                            }
                            Node<K,V> pred = e;
                            if ((e = e.next) == null) {
                                pred.next = new Node<K,V>(hash, key, value);
                                break;
                            }
                        }
                    }
                    //走红黑树节点的遍历判断，进行节点替换或者添加
                    else if (f instanceof TreeBin) {
                        Node<K,V> p;
                        binCount = 2;
                        if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
                                                              value)) != null) {
                            oldVal = p.val;
                            if (!onlyIfAbsent)
                                p.val = value;
                        }
                    }
                    else if (f instanceof ReservationNode)
                        throw new IllegalStateException("Recursive update");
                }
            }
            if (binCount != 0) {
                if (binCount >= TREEIFY_THRESHOLD)
                    treeifyBin(tab, i);
                if (oldVal != null)
                    return oldVal;
                break;
            }
        }
    }
    addCount(1L, binCount);
    return null;
}

jdk1.7ConcurrentHashMap源码简化

// 简化的JDK 1.7 ConcurrentHashMap结构
public class ConcurrentHashMap<K, V> {
    // 分段数组，默认大小为16
    final Segment<K,V>[] segments;
    

    // Segment类继承ReentrantLock，本身就是一种锁
    static final class Segment<K,V> extends ReentrantLock {
        // 每个Segment内部维护一个HashEntry数组
        transient volatile HashEntry<K,V>[] table;
        // 其他字段...
    }
    
    // 存储数据的节点
    static final class HashEntry<K,V> {
        final int hash;
        final K key;
        volatile V value;
        volatile HashEntry<K,V> next;
        // 构造函数等...
    }

}

(3)面试题

聊下ConcurrentHashMap

1.底层数据结构

jdk1.7采用分段数组+链表实现

jdk1.8采用跟HashMap一样的数据结构，数组+链表/红黑树

2.加锁方式

jdk1.7采用分段锁(Segment数组元素本身就继承了ReentrantLock)，使用的是ReentrantLock。

Jdk1.8在数组对应元素为null值时，使用CAS来添加新节点，元素不为null时，采用synchronized锁定链表或者红黑树的首节点

Segment分段锁，锁的是一个数组+链表的数据结构；而synchronized方式，锁的是一个链表或者红黑树，锁的粒度更细，性能更好。